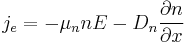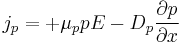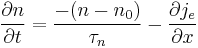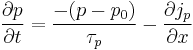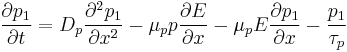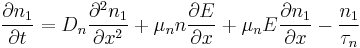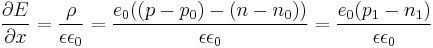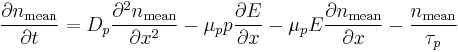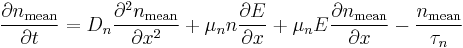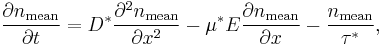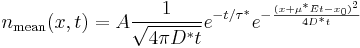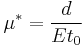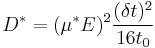Haynes–Shockley experiment
The Haynes–Shockley experiment was a classic experiment that demonstrated that diffusion of minority carriers in a semiconductor could result in a current. The experiment was reported in a paper by Shockley, Pearson, and Haynes in 1949.[1][2] The experiment can be used to measure carrier mobility, carrier lifetime, and diffusion coefficient.[3]
In the experiment, a piece of semiconductor gets a pulse of holes, for example, as induced by voltage or a short laser pulse.
To see the effect, we consider a n-type semiconductor with the length d. We are interested in determining the mobility of the carriers, diffusion constant and relaxation time. In the following, we reduce the problem to one dimension.
The equations for electron and hole currents are:
where the first part is the drift current and the second is the diffusion current.
We consider the continuity equation:
The electrons and the holes recombine with the time  .
.
We define 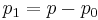 and
and 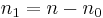 so the upper equations can be rewritten as:
so the upper equations can be rewritten as:
In a simple approximation, we can consider the electric field to be constant between the left and right electrodes and neglect 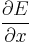 . However, as electrons and holes diffuse at a different speed, the material has a local electric charge, inducing an inhomogeneous electric field which can be calculated with Gauss's law:
. However, as electrons and holes diffuse at a different speed, the material has a local electric charge, inducing an inhomogeneous electric field which can be calculated with Gauss's law:
We make the following change of variables: 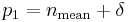 ,
, 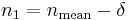 , and suppose
, and suppose 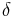 to be much smaller than
to be much smaller than 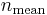 . The two initial equations write:
. The two initial equations write:
Thanks to Einstein relation 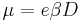 , these two equations can be combined:
, these two equations can be combined:
where for 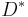 ,
, 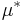 and
and 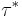 holds:
holds:
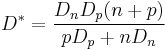 ,
, 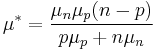 and
and 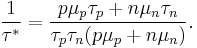
Considering n>>p or 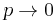 (that is a fair approximation for a semiconductor with only few holes injected), we see that
(that is a fair approximation for a semiconductor with only few holes injected), we see that 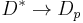 ,
, 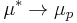 and
and 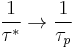 . The semiconductor behaves as if there were only holes traveling in it.
. The semiconductor behaves as if there were only holes traveling in it.
The final equation for the carriers is:
This can be interpreted as a delta function that is created immediately after the pulse. Holes then start to travel towards the electrode where we detect them. The signal then is Gaussian curve shaped.
Parameters 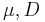 and
and  can be obtained from the shape of the signal.
can be obtained from the shape of the signal.
References
- ^ Shockley, W. and Pearson, G. L., and Haynes, J. R. (1949). "Hole injection in germanium – Quantitative studies and filamentary transistors". Bell System Technical Journal 28: 344–366.
- ^ Jerrold H. Krenz (2000). Electronic concepts: an introduction. Cambridge University Press. p. 137. ISBN 9780521662826. http://books.google.com/books?id=Le9zdVoMEOEC&pg=PA137.
- ^ Ajay Kumar Singh (2008). Electronic Devices And Integrated Circuits. PHI Learning Pvt. Ltd.. p. 119. ISBN 9788120331921. http://books.google.com/books?id=2aqtlybkFE0C&pg=PA119.